My colleagues organized a darts tournament at around the same time I watched the CS231n lecture about reinforcement learning. Of course, this could only end in one way - in a small reinforcement learning toy example.
The Rules
The darts game which we consider starts at 301 points. A player has three attempts in each turn. Every attempt reduces the initial score at the beginning of a turn. A player finishes the game if they land on exactly 0 points with a double field (the inner bullseye counts as double field). For example, if a player has 12 points remaining, they need to score a double 6 to finish the game. If a player ends up with a negative score, or a score of 0, but without hitting a double field, or a score of 1, they go bust and revert to the score at the beginning of their turn. The image below (source) shows how many points every field is worth.

The Problem
As nice as it would have been to simulate a robot arm and have it use a model-free learning algorithm, I made up a toy model with transition probabilities and used value iteration to learn the optimal policy. The coding can be found in this github repo under the folder value_iteration.
The board is modelled as an array which lists all fields starting from the top field in a clockwise manner. The fields are encoded as numbers from 0 to 81 (more about that later), whereas 82 completely misses the board. The scores associated to the field encodings can be obtained by accessing the SCORE array with the encoding as index.
BOARD = np.array([20, 1, 18, 4, 13, 9, 10, 15, 2, 17, 3, 19, 7, 16, 8, 11, 14, 9, 12, 5])
SCORE = np.concatenate((BOARD, BOARD, 2 * BOARD, 3 * BOARD, [25, 50, 0]))
Similarly to Baird (2018), we define the Markov Decision Problem with
- A set of states \(\mathcal{S} = \{ (s_0, s_k, k ) \vert s_0, s_k \in \{0,\ldots,301\}, k \in \{0,1,2\}, s_0 \ge s_k \ge s_0 - 60k\}\)
Every state \(S_t \in \mathcal{S}\) encodes the score at the beginning of a turn \(t\) to which the player returns should they go bust, the score before the \(k\)-th attempt and the attempt number \(k\). States with \(s_0 = 0\) or \(s_k\) = 0 are terminal states.
- A set of actions \(\mathcal{A} = \{0,\ldots,81\}\) with
- actions 0-19 encoding outer single fields
- actions 20-39 encoding inner single fields
- actions 40-59 encoding double fields
- actions 60-79 encoding treble fields
- action 80 encoding the outer bullseye
- action 81 encoding the bullseye
- For each new turn \(t\) a reward of \(-1\) is given. Otherwise, the reward is \(0\).
- The dynamics of the MDP (transition probabilities) are implicitly defined by the player’s skills. And this is where I got creative and modelled the player’s accuracy with made-up probability distributions (I am sure that the model player is pretty advanced). For example, if the model player aims for a specific outer single field \(x\), the actual field it hits is distributed as follows:
| where the arrow ends up at |
probability |
| outer single \(x\) |
92.00% |
| outer single neighbour left |
02.00% |
| outer single neighbour right |
02.00% |
| double \(x\) |
01.00% |
| treble \(x\) |
01.00% |
| double left neighbour |
00.50% |
| double right neighbour |
00.50% |
| treble left neighbour |
00.50% |
| treble right neighbour |
00.50% |
The complete model probabilities can be seen in the file darts.py.
The state values are kept in a 302x302x3x82 matrix. The matrix however, is sparse in the sense that you can only score a maximum of 60 points in a turn, so not all states in the matrix can be reached. All reachable states are initialized with zero. For each reachable action-state value, we repeat the Bellman update
\begin{align}
q_{k+1}(s,a) = \sum_{s’,r} p(S_{t+1}=s’,R_{t+1}=r \vert S_t=s, A_t = a)[r+\gamma \underset{a’}{\mathrm{max}} \ q_k(s’,a’)] \notag
\end{align}
until the difference between iterations is small enough. In my implementation (see value_iter.py), a total of 9 iterations was needed to converge for a chosen threshold of 0.01. If we plot the score associated with the optimal action against the state we are currently in (see qvalues.py), we get something like this:
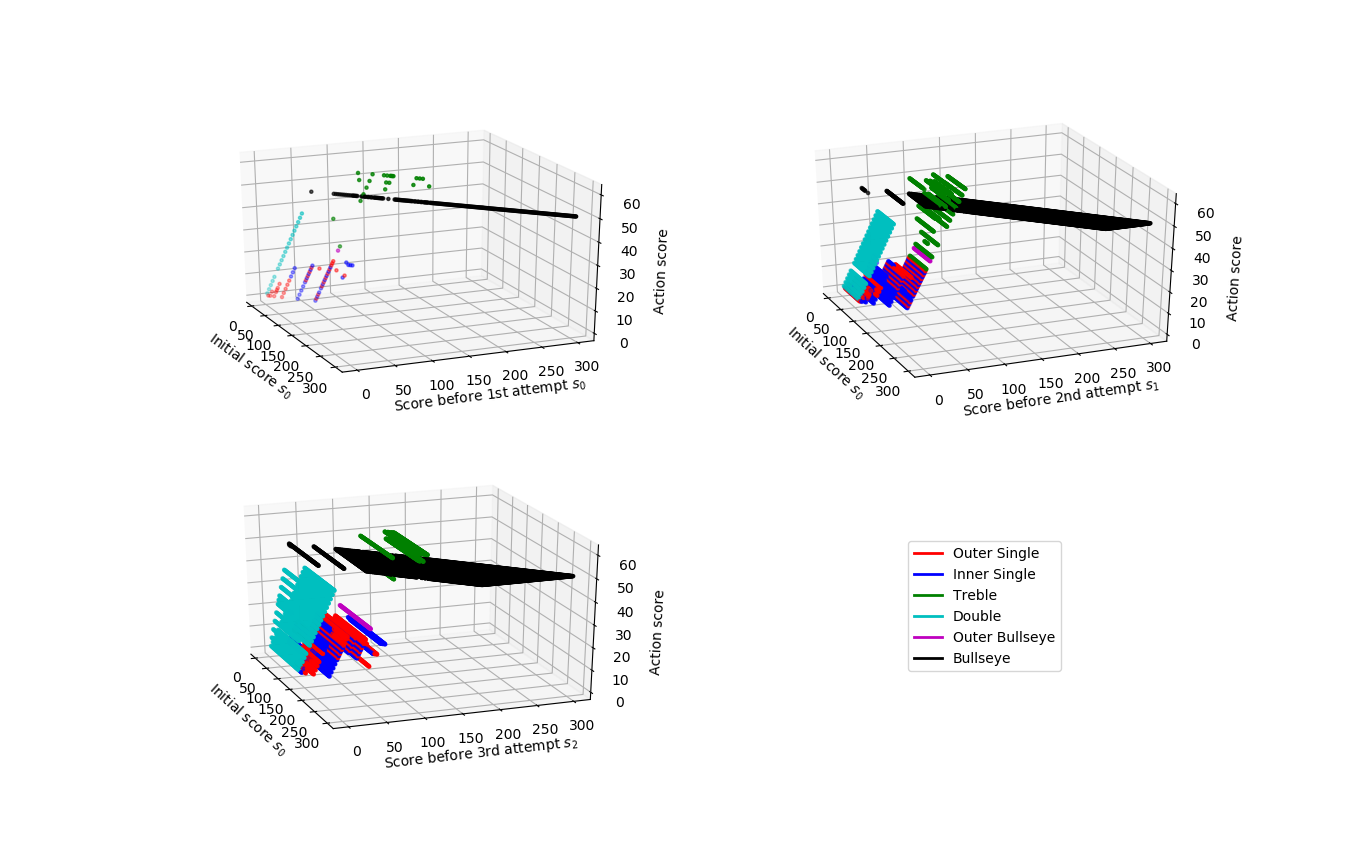
The optimal action for the model player is to almost always aim for inner bullseye, until the player approaches a score of around 50. When the player approaches a score of 50, they often aim for a target score of 50 because they can double out from there. Once the player drops below 50 points, popular target scores are 40, 36, 32, 16, 8, 4, 2 and 0 (if it is possible to double out). What’s surprising is that when the player has on odd score below 20 and is at their third attempt, then the optimal choice is to go bust. The reason could be that only the turns are penalized and not the attempts, so it makes no difference if the player tries again in the next turn (and doubles out in two attempts) or if they move to a lower score in the current turn and double out in the next turn.